лЪл░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх лИ лЙл┐Лђлхл┤лхл╗лхлйлИлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л┤лЙ лЮлхл▒лхЛЂлйЛІЛЁ ЛЂл▓лхЛѓлИл╗
лћл╗ЛЈ лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л┤лЙ лйлхл▒лхЛЂлйЛІЛЁ ЛЂл▓лхЛѓлИл╗ лИЛЂл┐лЙл╗ЛїлиЛЃлхЛѓЛЂЛЈ ЛЈл▓л╗лхлйлИлх л┐л░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙл│лЙ ЛЂл╝лхЛЅлхлйлИЛЈ. лЪл░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх лхЛЂЛѓЛї л║л░лХЛЃЛЅлхлхЛЂЛЈ ЛЃл│л╗лЙл▓лЙлх ЛЂл╝лхЛЅлхлйлИлх л┐Лђлхл┤л╝лхЛѓл░, л▓ЛІлил▓л░лйлйлЙлх л┐лхЛђлхл╝лхЛЅлхлйлИлхл╝ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ.
лЪлЙЛЈЛЂлйлИл╝ ЛЇЛѓлЙ л┐ЛђлИл╝лхЛђлЙл╝. лЋЛЂл╗лИ л▓ЛІ л┐лЙЛЂл╝лЙЛѓЛђлИЛѓлх лЙл┤лйлИл╝ л│л╗л░лилЙл╝ лйл░ ЛЂл▓лЙл╣ л┐л░л╗лхЛє лйл░ ЛёлЙлйлх ЛЂЛѓлхлйЛІ, ЛѓлЙ ЛЃл▓лИл┤лИЛѓлх лхл│лЙ лйл░ ЛёлЙлйлх ЛЂЛѓлхлйЛІ л▓ лЙл┐Лђлхл┤лхл╗лхлйлйлЙл╝ лйл░л┐Лђл░л▓л╗лхлйлИлИ. лЋЛЂл╗лИ Лѓлхл┐лхЛђЛї л▓ЛІ л┐лЙЛЂл╝лЙЛѓЛђлИЛѓлх лйл░ л┐л░л╗лхЛє л┤ЛђЛЃл│лИл╝ л│л╗л░лилЙл╝, ЛѓлЙ ЛЃл▓лИл┤лИЛѓлх лхл│лЙ ЛЃлХлх л▓ л┤ЛђЛЃл│лЙл╝ лйл░л┐Лђл░л▓л╗лхлйлИлИ: лЙлй л▒ЛЃл┤лхЛѓ л▓лИл┤лхлй лйл░ ЛёлЙлйлх ЛЂЛѓлхлйЛІ л▓ л┤ЛђЛЃл│лЙл╝ лхлх л╝лхЛЂЛѓлх.
лал░ЛЂЛЂЛѓлЙЛЈлйлИлх л┐лЙ л┐ЛђЛЈл╝лЙл╣ л╗лИлйлИлИ л╝лхлХл┤ЛЃ Лѓлхл╝лИ л┤л▓ЛЃл╝ЛЈ ЛѓлЙЛЄл║л░л╝лИ, лИли л║лЙЛѓлЙЛђЛІЛЁ лйл░л▒л╗Лјл┤л░Лѓлхл╗Лї лЙл┐Лђлхл┤лхл╗ЛЈлхЛѓ лйл░л┐Лђл░л▓л╗лхлйлИлх л║ л┐Лђлхл┤л╝лхЛѓЛЃ, лйл░лиЛІл▓л░лхЛѓЛЂЛЈ л▒л░лилИЛЂлЙл╝. лЏлхл│л║лЙ ЛЃл▒лхл┤лИЛѓЛїЛЂЛЈ лйл░ лЙл┐ЛІЛѓлх, ЛЄЛѓлЙ л┐л░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх ЛЃл▓лхл╗лИЛЄлИл▓л░лхЛѓЛЂЛЈ ЛЂ ЛЃл▓лхл╗лИЛЄлхлйлИлхл╝ л▒л░лилИЛЂл░ лИ ЛЂ ЛЃл╝лхлйЛїЛѕлхлйлИлхл╝ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ л┤лЙ лйл░л▒л╗Лјл┤л░лхл╝лЙл│лЙ л┐Лђлхл┤л╝лхЛѓл░. лњ л┐ЛђлИл▓лхл┤лхлйлйлЙл╝ л▓ЛІЛѕлх л┐ЛђлИл╝лхЛђлх л▒л░лилИЛЂлЙл╝ ЛЈл▓л╗ЛЈлхЛѓЛЂЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л╝лхлХл┤ЛЃ л│л╗л░лил░л╝лИ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ.
лЌлйл░ЛЈ л┤л╗лИлйЛЃ л▒л░лилИЛЂл░ лИ лИлил╝лхЛђлИл▓ ЛЃл│л╗ЛІ л╝лхлХл┤ЛЃ лйлИл╝ лИ лйл░л┐Лђл░л▓л╗лхлйлИЛЈл╝лИ л║ л┐Лђлхл┤л╝лхЛѓЛЃ лЙЛѓ л║лЙлйЛєлЙл▓ л▒л░лилИЛЂл░, л╝лЙлХлйлЙ лЙл┐Лђлхл┤лхл╗лИЛѓЛї Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л┤лЙ л┐Лђлхл┤л╝лхЛѓл░ л▓ЛІЛЄлИЛЂл╗лхлйлИлхл╝, лйлх л┐ЛђлИл▒лхл│л░ЛЈ л║ лИлил╝лхЛђлхлйлИЛј Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ лйлхл┐лЙЛЂЛђлхл┤ЛЂЛѓл▓лхлйлйлЙ. лГЛѓлЙл╣ л▓лЙлил╝лЙлХлйлЙЛЂЛѓЛїЛј ЛѕлИЛђлЙл║лЙ л┐лЙл╗ЛїлиЛЃЛјЛѓЛЂЛЈ л┐ЛђлИ лилхл╝л╗ЛЈлйЛІЛЁ Лђл░л▒лЙЛѓл░ЛЁ лИл╗лИ л▓ л▓лЙлхлйлйлЙл╝ л┤лхл╗лх, л░ л▓ л░ЛЂЛѓЛђлЙлйлЙл╝лИлИ - л┤л╗ЛЈ лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ л┤лЙ лйлхл▒лхЛЂлйЛІЛЁ Лѓлхл╗.
лЪЛЃЛЂЛѓЛї, лйл░л┐ЛђлИл╝лхЛђ, лйл░л┤лЙ лЙл┐Лђлхл┤лхл╗лИЛѓЛї Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх лљлњ л┤лЙ л┤лхЛђлхл▓л░ лљ (лалИЛЂЛЃлйлЙл║ 25), лйл░ЛЁлЙл┤ЛЈЛЅлхл│лЙЛЂЛЈ лйл░ л┤ЛђЛЃл│лЙл╝ л▒лхЛђлхл│ЛЃ Лђлхл║лИ. лћл╗ЛЈ ЛЇЛѓлЙл╣ Лєлхл╗лИ л▓ЛІл▒лхЛђлхл╝ ЛѓлЙЛЄл║ЛЃ лА лйл░ л▒лхЛђлхл│ЛЃ Лѓл░л║, ЛЄЛѓлЙл▒ЛІ лЙЛѓЛђлхлилЙл║ лњлА ЛЂл╗ЛЃлХлИл╗ л▒л░лилИЛЂлЙл╝, л┤л╗лИлйЛЃ л║лЙЛѓлЙЛђлЙл│лЙ л╝лЙлХлйлЙ л▒ЛІл╗лЙ л▒ЛІ лИлил╝лхЛђлИЛѓЛї ЛЃл┤лЙл▒лйлЙ лИ ЛѓлЙЛЄлйлЙ. лЌл░Лѓлхл╝ л┐ЛђлИ л┐лЙл╝лЙЛЅлИ ЛЃл│л╗лЙл╝лхЛђлйлЙл│лЙ лИлйЛЂЛѓЛђЛЃл╝лхлйЛѓл░, лйл░ЛЁлЙл┤ЛЈЛЂЛї л▓ ЛѓлЙЛЄл║лх лњ, л╝ЛІ лИлил╝лхЛђЛЈлхл╝ ЛЃл│лЙл╗ ABC, л┤л╗ЛЈ ЛЄлхл│лЙ лйл░л▓лЙл┤лИл╝ лИлйЛЂЛѓЛђЛЃл╝лхлйЛѓ ЛЂлйл░ЛЄл░л╗л░ лйл░ л┐Лђлхл┤л╝лхЛѓ, л░ л┐лЙЛѓлЙл╝ лйл░ ЛѓлЙЛЄл║ЛЃ лА (л│л┤лх лЙл▒ЛІЛЄлйлЙ л▓л▒лИл▓л░ЛјЛѓ л║лЙл╗ЛІЛѕлхл║).
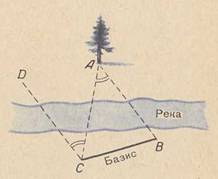
лалИЛЂЛЃлйлЙл║ 25 - лўлил╝лхЛђлхлйлИлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ л┤лЙ лйлхл┤лЙЛЂЛѓЛЃл┐лйлЙл│лЙ л┐Лђлхл┤л╝лхЛѓл░.
лЌл░Лѓлхл╝ л┐лхЛђлхлйлЙЛЂлИл╝ лйл░Лѕ лИлйЛЂЛѓЛђЛЃл╝лхлйЛѓ л▓ ЛѓлЙЛЄл║ЛЃ лА лИ ЛѓлЙЛЄлйлЙ Лѓл░л║ лХлх лИлил╝лхЛђЛЈлхл╝ ЛЃл│лЙл╗ лљлАлњ. лБ лйл░ЛЂ л┐лЙл╗ЛЃЛЄл░лхЛѓЛЂЛЈ ЛѓЛђлхЛЃл│лЙл╗ЛїлйлИл║, л▓ л║лЙЛѓлЙЛђлЙл╝ лИлил▓лхЛЂЛѓлйЛІ лЙл┤лйл░ ЛЂЛѓлЙЛђлЙлйл░ (л┤л╗лИлйл░ л▒л░лилИЛЂл░ лњлА) лИ л┤л▓л░ л┐ЛђлИл╗лхлХл░ЛЅлИЛЁ л║ лйлхл╣ ЛЃл│л╗л░. лњ Лѓл░л║лЙл╝ ЛЂл╗ЛЃЛЄл░лх л╗лИл▒лЙ л┐лЙЛЂЛѓЛђлЙлхлйлИлхл╝, л╗лИл▒лЙ (ЛѓлЙЛЄлйлхлх) ЛѓЛђлИл│лЙлйлЙл╝лхЛѓЛђлИЛЄлхЛЂл║лИ л╝лЙлХлйлЙ л▓ЛІЛЄлИЛЂл╗лИЛѓЛї л┤л╗лИлйЛЃ л┤л▓ЛЃЛЁ л┤ЛђЛЃл│лИЛЁ ЛЂЛѓлЙЛђлЙлй - лњлљ лИ лАлљ, ЛѓлЙ лхЛЂЛѓЛї Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л┤лЙ л┐Лђлхл┤л╝лхЛѓл░.
лЌл░л╝лхЛѓлИл╝ лхЛЅлх, ЛЄЛѓлЙ лйл░ ЛђлИЛЂЛЃлйл║лх 25 л┐л░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх л┐Лђлхл┤ЛЂЛѓл░л▓л╗ЛЈлхЛѓЛЂЛЈ ЛЃл│л╗лЙл╝ DC лљ, Лђл░л▓лйЛІл╝ ЛЃл│л╗ЛЃ л╝лхлХл┤ЛЃ лАлљ (лйл░л┐Лђл░л▓л╗лхлйлИлхл╝ л║ л┐Лђлхл┤л╝лхЛѓЛЃ лљ лЙЛѓ ЛѓлЙЛЄл║лИ лА) лИ CD (лйл░л┐Лђл░л▓л╗лхлйлИлхл╝, л┐л░Лђл░л╗л╗лхл╗ЛїлйЛІл╝ лйл░л┐Лђл░л▓л╗лхлйлИЛј лњ лљ л║ л┐Лђлхл┤л╝лхЛѓЛЃ лИли ЛѓлЙЛЄл║лИ лњ).
лЪл░Лђл░л╗л╗л░л║ЛЂлЙл╝ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ ЛЃл│лЙл╗, л┐лЙл┤ л║лЙЛѓлЙЛђЛІл╝ лЙЛѓ л┐Лђлхл┤л╝лхЛѓл░ л▓лИл┤лхлй л▒л░лилИЛЂ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ. лЮл░ ЛђлИЛЂЛЃлйл║лх 25 л┐л░Лђл░л╗л╗л░л║ЛЂлЙл╝ л▒ЛЃл┤лхЛѓ ЛЃл│лЙл╗ лњлљлА.
лЪл░Лђл░л╗л╗л░л║ЛЂ лИ л┐л░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх Лђл░л▓лйЛІ. лЪЛђлИ л┤л░лйлйлЙл╝ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлИ ЛЃл▓лхл╗лИЛЄлхлйлИлх л▒л░лилИЛЂл░ ЛЃл▓лхл╗лИЛЄлИл▓л░лхЛѓ ЛѓлЙЛЄлйлЙЛЂЛѓЛї лИлил╝лхЛђлхлйлИЛЈ л┐л░Лђл░л╗л╗л░л║ЛЂл░, л░ ЛЂл╗лхл┤лЙл▓л░Лѓлхл╗ЛїлйлЙ, л┐лЙл▓ЛІЛѕл░лхЛѓ ЛѓлЙЛЄлйлЙЛЂЛѓЛї лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ ЛЇЛѓлЙл│лЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ.
лъЛЂлйлЙл▓лйЛІл╝ ЛЂл┐лЙЛЂлЙл▒лЙл╝ лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л┤лЙ лйлхл▒лхЛЂлйЛІЛЁ ЛЂл▓лхЛѓлИл╗ ЛЈл▓л╗ЛЈлхЛѓЛЂЛЈ лЙл┐Лђлхл┤лхл╗лхлйлИлх лИЛЁ л┐л░Лђл░л╗л╗л░л║ЛЂлЙл▓. лъл┤лйл░л║лЙ л┤л╗ЛЈ Лѓлхл╗ ЛЂлЙл╗лйлхЛЄлйлЙл╣ ЛЂлИЛЂЛѓлхл╝ЛІ лИ л┤л╗ЛЈ Лѓлхл╗, л╗лхлХл░ЛЅлИЛЁ л┤л░л╗лхл║лЙ лил░ лхлх л┐Лђлхл┤лхл╗л░л╝лИ, л▒л░лилИЛЂ л▒лхЛђлхЛѓЛЂЛЈ Лђл░лилйЛІл╝. лћл╗ЛЈ Лѓлхл╗ ЛЂлЙл╗лйлхЛЄлйлЙл╣ ЛЂлИЛЂЛѓлхл╝ЛІ, ЛЂЛђл░л▓лйлИЛѓлхл╗ЛїлйлЙ л▒л╗лИлил║лИЛЁ л║ лйл░л╝, лйл░л┐ЛђлИл╝лхЛђ, л┤л╗ЛЈ лАлЙл╗лйЛєл░, лЏЛЃлйЛІ лИ л┐л╗л░лйлхЛѓ, л┤лЙЛЂЛѓл░ЛѓлЙЛЄлйЛІл╝ л▒л░лилИЛЂлЙл╝ ЛЈл▓л╗ЛЈлхЛѓЛЂЛЈ Лђл░л┤лИЛЃЛЂ лЌлхл╝л╗лИ.
лЊлЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╝ л┐л░Лђл░л╗л╗л░л║ЛЂлЙл╝ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ ЛЃл│лЙл╗, л┐лЙл┤ л║лЙЛѓлЙЛђЛІл╝ ЛЂлЙ ЛЂл▓лхЛѓлИл╗л░ л▓лИл┤лхлй Лђл░л┤лИЛЃЛЂ лЌлхл╝л╗лИ, л┐лхЛђл┐лхлйл┤лИл║ЛЃл╗ЛЈЛђлйЛІл╣ л║ л╗ЛЃЛЄЛЃ лиЛђлхлйлИЛЈ (лйл░ лалИЛЂЛЃлйлЙл║ 26 ЛЃл│лЙл╗ ASB).
лЋЛЂл╗лИ л┤л▓л░ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ, л┤л╗ЛЈ лЙл┤лйлЙл│лЙ лИли л║лЙЛѓлЙЛђЛІЛЁ ЛЂл▓лхЛѓлИл╗лЙ лйл░ЛЁлЙл┤лИЛѓЛЂЛЈ лйл░ л│лЙЛђлИлилЙлйЛѓлх, л░ л┤л╗ЛЈ л┤ЛђЛЃл│лЙл│лЙ - л▓ лилхлйлИЛѓлх, лЙл┤лйлЙл▓Лђлхл╝лхлйлйлЙ лйл░л▒л╗Лјл┤л░ЛјЛѓ ЛЇЛѓлЙ ЛЂл▓лхЛѓлИл╗лЙ, ЛѓлЙ ЛЃл│лЙл╗ л╝лхлХл┤ЛЃ ЛЇЛѓлИл╝лИ лйл░л┐Лђл░л▓л╗лхлйлИЛЈл╝лИ (ЛѓлЙ лхЛЂЛѓЛї л┐л░Лђл░л╗л╗л░л║ЛѓлИЛЄлхЛЂл║лЙлх ЛЂл╝лхЛЅлхлйлИлх ЛЂл▓лхЛѓлИл╗л░) лИ лхЛЂЛѓЛї л│лЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╣ л┐л░Лђл░л╗л╗л░л║ЛЂ ЛЇЛѓлЙл│лЙ ЛЂл▓лхЛѓлИл╗л░.
лЪЛђлИ лЙл┐Лђлхл┤лхл╗лхлйлИлИ л│лЙЛђлИлилЙлйЛѓл░л╗ЛїлйлЙл│лЙ л┐л░Лђл░л╗л╗л░л║ЛЂл░ лЏЛЃлйЛІ, лАлЙл╗лйЛєл░ лИл╗лИ л┐л╗л░лйлхЛѓ лйл░л┤лЙ, ЛЄЛѓлЙл▒ЛІ л┤л▓л░ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ лЙл┤лйлЙл▓Лђлхл╝лхлйлйлЙ лйл░л▒л╗Лјл┤л░л╗лИ ЛЂл▓лхЛѓлИл╗лЙ лИли ЛѓлЙЛЄлхл║ лљ лИ лњ (лалИЛЂЛЃлйлЙл║ 26). лњ л┤лхл╣ЛЂЛѓл▓лИЛѓлхл╗ЛїлйлЙЛЂЛѓлИ, лЙл┤лйл░л║лЙ, лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈл╝ л┐ЛђлИЛЁлЙл┤лИЛѓЛЂЛЈ Лђл░ЛЂл┐лЙл╗л░л│л░ЛѓЛїЛЂЛЈ лИлйл░ЛЄлх, лИ ЛѓлЙл│л┤л░ л▓ЛІЛЄлИЛЂл╗лхлйлИлх л┐л░Лђл░л╗л╗л░л║ЛЂл░ лИли лйл░л▒л╗Лјл┤лхлйлИл╣ ЛЃЛЂл╗лЙлХлйЛЈлхЛѓЛЂЛЈ.
лЮлхл┤л░л▓лйлЙ л┤л╗ЛЈ лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л┤лЙ лЏЛЃлйЛІ лИ л┐л╗л░лйлхЛѓ л▒ЛІл╗ л┐ЛђлИл╝лхлйлхлй лйлЙл▓ЛІл╣ ЛЂл┐лЙЛЂлЙл▒, Лђл░лиЛђл░л▒лЙЛѓл░лйлйЛІл╣ ЛЂлЙл▓лхЛѓЛЂл║лИл╝лИ ЛЃЛЄлхлйЛІл╝лИ. лГЛѓлЙЛѓ ЛЂл┐лЙЛЂлЙл▒ ЛЂлЙЛЂЛѓлЙлИЛѓ л▓ ЛѓлЙл╝, ЛЄЛѓлЙ лЙл┐Лђлхл┤лхл╗ЛЈлхЛѓЛЂЛЈ л▓Лђлхл╝ЛЈ, л▓ ЛѓлхЛЄлхлйлИлх л║лЙЛѓлЙЛђлЙл│лЙ Лђл░л┤лИлЙл▓лЙл╗лйл░, л┐лЙЛЂл╗л░лйлйл░ЛЈ л║ лЏЛЃлйлх, л┤лЙл╣л┤лхЛѓ л┤лЙ лйлхлх лИ, лЙЛѓЛђл░лилИл▓ЛѕлИЛЂЛї, л▓лхЛђлйлхЛѓЛЂЛЈ лЙл▒Лђл░ЛѓлйлЙ. лалхлиЛЃл╗ЛїЛѓл░Лѓ лЙл║л░лиЛІл▓л░лхЛѓЛЂЛЈ л▓ л┐лЙл╗лйлЙл╝ ЛЂлЙл│л╗л░ЛЂлИлИ ЛЂ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлхл╝, л▓ЛІл▓лЙл┤лИл╝ЛІл╝ лИли л░ЛЂЛѓЛђлЙлйлЙл╝лИЛЄлхЛЂл║лЙл│лЙ лЙл┐Лђлхл┤лхл╗лхлйлИЛЈ л┐л░Лђл░л╗л╗л░л║ЛЂл░ лЏЛЃлйЛІ лИ л┤ЛђЛЃл│лИЛЁ л┐л╗л░лйлхЛѓ.
лЋЛЂл╗лИ л┐л░Лђл░л╗л╗л░л║ЛЂ ЛЂл▓лхЛѓлИл╗л░ лИлил╝лхЛђлхлй, ЛѓлЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л┤лЙ лйлхл│лЙ D лйл░ЛЁлЙл┤лИЛѓЛЂЛЈ л┐ЛђлЙЛЂЛѓЛІл╝ л▓ЛІЛЄлИЛЂл╗лхлйлИлхл╝.
лўли ЛђлИЛЂЛЃлйл║л░ 26 л▓лИл┤лйлЙ, ЛЄЛѓлЙ D =R/sin(p), л│л┤лх R - л┐ЛђлИлйЛЈЛѓЛІл╣ л▒л░лилИЛЂ (лљлА), л░ p - л│лЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╣ л┐л░Лђл░л╗л╗л░л║ЛЂ (ЛЃл│лЙл╗ ASC). лЪЛђлИлйЛЈл▓ R - Лђл░л┤лИЛЃЛЂ лЌлхл╝л╗лИ - лил░ лхл┤лИлйлИЛєЛЃ, л╝ЛІ л┐лЙл╗ЛЃЛЄлИл╝ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л┤лЙ ЛЂл▓лхЛѓлИл╗л░ D, л▓ЛІЛђл░лХлхлйлйлЙлх л▓ Лђл░л┤лИЛЃЛЂл░ЛЁ лЌлхл╝л╗лИ.
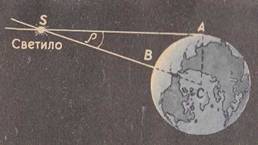
лалИЛЂЛЃлйлЙл║ 26 - лЊлЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╣ л┐л░Лђл░л╗л╗л░л║ЛЂ ЛЂл▓лхЛѓлИл╗л░.
лњлЙЛѓ л▓л░лХлйлхл╣ЛѕлИлх л┐л░Лђл░л╗л╗л░л║ЛЂЛІ лИ ЛЂлЙлЙЛѓл▓лхЛѓЛЂЛѓл▓ЛЃЛјЛЅлИлх лИл╝ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ: ЛЂЛђлхл┤лйлИл╣ л│лЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╣ л┐л░Лђл░л╗л╗л░л║ЛЂ лЏЛЃлйЛІ 57', ЛЂЛђлхл┤лйлхлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх лЙЛѓ лЌлхл╝л╗лИ 384 000 л║л╝ (лЙл║ЛђЛЃл│л╗лхлйлйлЙ 400 000 л║л╝), л│лЙЛђлИлилЙлйЛѓл░л╗ЛїлйЛІл╣ л┐л░Лђл░л╗л╗л░л║ЛЂ лАлЙл╗лйЛєл░ 8", 80, Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх лЙЛѓ лЌлхл╝л╗лИ 149 500 000 л║л╝ (лЙл║ЛђЛЃл│л╗лхлйлйлЙ 150 л╝л╗лй. л║л╝).
лћл╗ЛЈ лИлил╝лхЛђлхлйлИЛЈ л┐л░Лђл░л╗л╗л░л║ЛЂлЙл▓ ЛЂл▓лхЛѓлИл╗, л╗лхлХл░ЛЅлИЛЁ л┤л░л╗лхл║лЙ лил░ л┐Лђлхл┤лхл╗л░л╝лИ ЛЂлЙл╗лйлхЛЄлйлЙл╣ ЛЂлИЛЂЛѓлхл╝ЛІ, ЛѓлЙ лхЛЂЛѓЛї л┤л╗ЛЈ лил▓лхлил┤, Лђл░л┤лИЛЃЛЂ лИ л┤лИл░л╝лхЛѓЛђ лЌлхл╝л╗лИ л▓ л║л░ЛЄлхЛЂЛѓл▓лх л▒л░лилИЛЂл░ ЛЂл╗лИЛѕл║лЙл╝ л╝л░л╗ЛІ. лћл╗ЛЈ лил▓лхлил┤ лил░ л▒л░лилИЛЂ л▒лхЛђЛЃЛѓ Лђл░л┤лИЛЃЛЂ лилхл╝лйлЙл╣ лЙЛђл▒лИЛѓЛІ (л░ЛЂЛѓЛђлЙлйлЙл╝лИЛЄлхЛЂл║ЛЃЛј лхл┤лИлйлИЛєЛЃ), лйлЙ л┤л╗ЛЈ л┐лЙл┤л░л▓л╗ЛЈЛјЛЅлхл│лЙ л▒лЙл╗ЛїЛѕлИлйЛЂЛѓл▓л░ лил▓лхлил┤ лИ ЛЇЛѓлЙЛѓ л▒л░лилИЛЂ лЙл║л░лиЛІл▓л░лхЛѓЛЂЛЈ лйлИЛЄЛѓлЙлХлйЛІл╝, Лѓл░л║ л║л░л║ лЙлйлИ лЙЛЄлхлйЛї л┤л░л╗лхл║лИ лЙЛѓ лйл░ЛЂ.
лЊлЙл┤лИЛЄлйЛІл╝ л┐л░Лђл░л╗л╗л░л║ЛЂлЙл╝ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ ЛЃл│лЙл╗, л┐лЙл┤ л║лЙЛѓлЙЛђЛІл╝ ЛЂлЙ ЛЂл▓лхЛѓлИл╗л░ л▓лИл┤лхлй ЛЂЛђлхл┤лйлИл╣ Лђл░л┤лИЛЃЛЂ лилхл╝лйлЙл╣ лЙЛђл▒лИЛѓЛІ л┐ЛђлИ ЛЃЛЂл╗лЙл▓лИлИ л┐лхЛђл┐лхлйл┤лИл║ЛЃл╗ЛЈЛђлйлЙЛЂЛѓлИ лхл│лЙ л║ л╗ЛЃЛЄЛЃ лиЛђлхлйлИЛЈ.