лўЛЂЛѓлИлйлйлЙлх л┤л▓лИлХлхлйлИлх л┐л╗л░лйлхЛѓ лИ лил░л║лЙлйЛІ лџлхл┐л╗лхЛђл░
лњлИл┤лИл╝ЛІлх л┐лхЛѓл╗лхлЙл▒Лђл░лилйЛІлх л┤л▓лИлХлхлйлИЛЈ л┐л╗л░лйлхЛѓ лџлЙл┐лхЛђлйлИл║ лЙл▒ЛіЛЈЛЂлйЛЈл╗ ЛЂлЙЛЄлхЛѓл░лйлИлхл╝ л┤л▓лИлХлхлйлИЛЈ лЌлхл╝л╗лИ ЛЂ л┤л▓лИлХлхлйлИлхл╝ л║л░лХл┤лЙл╣ л┐л╗л░лйлхЛѓЛІ л▓лЙл║ЛђЛЃл│ лАлЙл╗лйЛєл░. лбл░л║ л║л░л║ л┐лхЛђлИлЙл┤ЛІ лЙл▒Лђл░ЛЅлхлйлИЛЈ лЌлхл╝л╗лИ лИ л╗Лјл▒лЙл╣ л┐л╗л░лйлхЛѓЛІ лйлхлЙл┤лИлйл░л║лЙл▓ЛІ, ЛѓлЙ л▒ЛІл▓л░лхЛѓ, ЛЄЛѓлЙ, лйл░л┐ЛђлИл╝лхЛђ, лЌлхл╝л╗ЛЈ лЙл▒л│лЙлйЛЈлхЛѓ л┐л╗л░лйлхЛѓЛЃ, лИ ЛѓлЙл│л┤л░ л┐л╗л░лйлхЛѓл░ л║л░лХлхЛѓЛЂЛЈ ЛЂл╝лхЛЅл░ЛјЛЅлхл╣ЛЂЛЈ лЙЛѓлйлЙЛЂлИЛѓлхл╗ЛїлйлЙ лил▓лхлил┤ л║ лил░л┐л░л┤ЛЃ. лњ л┤ЛђЛЃл│лЙлх лХлх л▓Лђлхл╝ЛЈ л┤л▓лИлХлхлйлИЛЈ лИЛЁ ЛЂл║л╗л░л┤ЛІл▓л░ЛјЛѓЛЂЛЈ Лѓл░л║, ЛЄЛѓлЙ л┐л╗л░лйлхЛѓл░ л║л░лХлхЛѓЛЂЛЈ л┐лхЛђлхл╝лхЛЅл░ЛјЛЅлхл╣ЛЂЛЈ л║ л▓лЙЛЂЛѓлЙл║ЛЃ.
лГЛѓлЙ л┐лЙЛЈЛЂлйЛЈлхЛѓ ЛђлИЛЂЛЃлйлЙл║ 20, л│л┤лх ЛЂЛѓЛђлхл╗л║лИ л┐лЙл║л░лиЛІл▓л░ЛјЛѓ лйл░л┐Лђл░л▓л╗лхлйлИлх лЙл▒Лђл░ЛЅлхлйлИЛЈ лЌлхл╝л╗лИ лИ л┐л╗л░лйлхЛѓЛІ, л║лЙЛѓлЙЛђл░ЛЈ л┤л░л╗ЛїЛѕлх лЙЛѓ лАлЙл╗лйЛєл░, ЛЄлхл╝ лЌлхл╝л╗ЛЈ, лИ л┤л▓лИлХлхЛѓЛЂЛЈ л╝лхл┤л╗лхлйлйлхлх. лЪЛђЛЈл╝ЛІлх л╗лИлйлИлИ ЛЂлЙлхл┤лИлйЛЈЛјЛѓ лЙл┤лйлЙл▓Лђлхл╝лхлйлйЛІлх л┐лЙл╗лЙлХлхлйлИЛЈ лЌлхл╝л╗лИ лИ л┐л╗л░лйлхЛѓЛІ лИ ЛЃл║л░лиЛІл▓л░ЛјЛѓ лйл░л┐Лђл░л▓л╗лхлйлИлх, л┐лЙ л║лЙЛѓлЙЛђлЙл╝ЛЃ л┐л╗л░лйлхЛѓл░ л▓лИл┤лйл░ ЛЂ лЌлхл╝л╗лИ л┐ЛђлИ Лђл░лилйЛІЛЁ лхлх л┐лЙл╗лЙлХлхлйлИЛЈЛЁ лйл░ лЙЛђл▒лИЛѓлх. лАЛѓЛђлхл╗л║лИ ЛЃ л▓лИл┤лИл╝лЙл│лЙ л┐ЛЃЛѓлИ л┐л╗л░лйлхЛѓЛІ л┐лЙл║л░лиЛІл▓л░ЛјЛѓ, л║л░л║ л┐ЛђлИ ЛЇЛѓлЙл╝ л╝лхлйЛЈлхЛѓЛЂЛЈ лйл░л┐Лђл░л▓л╗лхлйлИлх лхлх л▓лИл┤лИл╝лЙл│лЙ л┤л▓лИлХлхлйлИЛЈ.
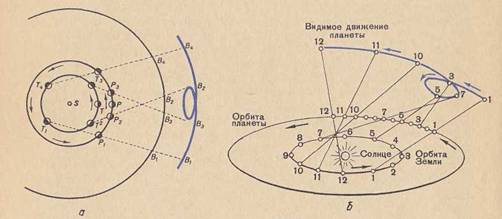
лалИЛЂЛЃлйлЙл║ 20 - лњлИл┤лИл╝лЙлх л┐лхЛѓл╗лхлЙл▒Лђл░лилйлЙлх л┤л▓лИлХлхлйлИлх л┐л╗л░лйлхЛѓЛІ (л┐ЛђлЙлИЛЂЛЁлЙл┤лИЛѓ л▓ЛЂл╗лхл┤ЛЂЛѓл▓лИлх ЛЂлЙЛЄлхЛѓл░лйлИЛЈ л┤л▓лИлХлхлйлИЛЈ л┐л╗л░лйлхЛѓЛІ лИ лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ л▓л╝лхЛЂЛѓлх ЛЂ лЌлхл╝л╗лхл╣).
лџлЙл┐лхЛђлйлИл║ лЙл┐Лђлхл┤лхл╗лИл╗ л┐лхЛђлИлЙл┤ЛІ лЙл▒Лђл░ЛЅлхлйлИЛЈ л┐л╗л░лйлхЛѓ лИ лИЛЁ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ лЙЛѓ лАлЙл╗лйЛєл░ л┐лЙ ЛЂЛђл░л▓лйлхлйлИЛј ЛЂ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлхл╝ лЌлхл╝л╗лИ лЙЛѓ лАлЙл╗лйЛєл░.
лњлил░лИл╝лйлЙлх Лђл░ЛЂл┐лЙл╗лЙлХлхлйлИлх лЌлхл╝л╗лИ лИ л┐л╗л░лйлхЛѓ л▓ЛЂлх л▓Лђлхл╝ЛЈ л╝лхлйЛЈлхЛѓЛЂЛЈ. лЮл░л┐ЛђлИл╝лхЛђ, л┐л╗л░лйлхЛѓл░, л▒лЙл╗лхлх л┤л░л╗лхл║л░ЛЈ лЙЛѓ лАлЙл╗лйЛєл░, ЛЄлхл╝ лЌлхл╝л╗ЛЈ, л┐лЙ лЙЛѓлйлЙЛѕлхлйлИЛј л║ л┐лЙЛЂл╗лхл┤лйлхл╣ л╝лЙлХлхЛѓ л▒ЛІЛѓЛї лил░ лАлЙл╗лйЛєлхл╝ (лалИЛЂЛЃлйлЙл║ 21), л░ л┐л╗л░лйлхЛѓл░, л▒лЙл╗лхлх л▒л╗лИлил║л░ЛЈ,- л╝лхлХл┤ЛЃ лЌлхл╝л╗лхл╣ лИ лАлЙл╗лйЛєлхл╝ лИл╗лИ ЛѓлЙлХлх лил░ лйлИл╝. лњ ЛЇЛѓлИЛЁ л┐лЙл╗лЙлХлхлйлИЛЈЛЁ л┐л╗л░лйлхЛѓЛІ лйл░л╝ лйлх л▓лИл┤лйЛІ, Лѓл░л║ л║л░л║ ЛЂл║ЛђЛІл▓л░ЛјЛѓЛЂЛЈ л▓ л╗ЛЃЛЄл░ЛЁ лАлЙл╗лйЛєл░. лЪл╗л░лйлхЛѓЛЃ, л▒лЙл╗лхлх л┤л░л╗лхл║ЛЃЛј лЙЛѓ лАлЙл╗лйЛєл░, ЛЄлхл╝ лЌлхл╝л╗ЛЈ, л╗ЛЃЛЄЛѕлх л▓ЛЂлхл│лЙ лйл░л▒л╗Лјл┤л░ЛѓЛї, л║лЙл│л┤л░ лЙлйл░ л▓лИл┤лйл░ л▓ ЛЂЛѓлЙЛђлЙлйлх, л┐ЛђлЙЛѓлИл▓лЙл┐лЙл╗лЙлХлйлЙл╣ лАлЙл╗лйЛєЛЃ. лблЙл│л┤л░ лЙлйл░ л▒л╗лИлХлх л║ лЌлхл╝л╗лх лИ ЛЁлЙЛђлЙЛѕлЙ л▓лИл┤лйл░ л▓ Лѓлхл╗лхЛЂл║лЙл┐. лњ ЛЇЛѓЛЃ л┐лЙЛђЛЃ лЙлйл░ л║ЛЃл╗Лїл╝лИлйлИЛђЛЃлхЛѓ л▓ л┐лЙл╗лйлЙЛЄЛї лИ л┤лЙл╗л│лЙ л▓лИл┤лйл░ л▓ ЛѓлхЛЄлхлйлИлх л┤лйЛЈ. лЪлЙл╗лЙлХлхлйлИлх л┐л╗л░лйлхЛѓЛІ, л┐ЛђлЙЛѓлИл▓лЙл┐лЙл╗лЙлХлйлЙлх лАлЙл╗лйЛєЛЃ л┐лЙ лЙЛѓлйлЙЛѕлхлйлИЛј л║ лЌлхл╝л╗лх, лйл░лиЛІл▓л░лхЛѓЛЂЛЈ л┐ЛђлЙЛѓлИл▓лЙЛЂЛѓлЙЛЈлйлИлхл╝.
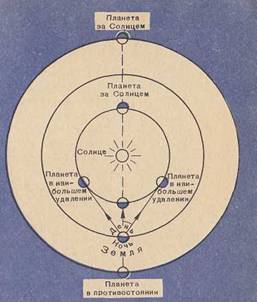
лалИЛЂЛЃлйлЙл║ 21 - лЪЛђлЙЛѓлИл▓лЙЛЂЛѓлЙЛЈлйлИЛЈ лИ лйл░лИл▒лЙл╗ЛїЛѕлИлх ЛЃл┤л░л╗лхлйлИЛЈ л┐л╗л░лйлхЛѓЛІ лЙЛѓ лАлЙл╗лйЛєл░.
лћл╗ЛЈ л┐л╗л░лйлхЛѓЛІ, л▒лЙл╗лхлх л▒л╗лИлил║лЙл╣ л║ лАлЙл╗лйЛєЛЃ, ЛЄлхл╝ лЌлхл╝л╗ЛЈ, ЛЃл│лЙл╗ л╝лхлХл┤ЛЃ лйл░л┐Лђл░л▓л╗лхлйлИЛЈл╝лИ ЛЂ лЌлхл╝л╗лИ лйл░ лйлхлх лИ лйл░ лАлЙл╗лйЛєлх л╝лхлйЛЈлхЛѓЛЂЛЈ, лйлх л┐Лђлхл▓лЙЛЂЛЁлЙл┤ЛЈ 29°л┤л╗ЛЈ люлхЛђл║ЛЃЛђлИЛЈ лИ 48° л┤л╗ЛЈ лњлхлйлхЛђЛІ. лЪЛђлИ лйл░лИл▒лЙл╗ЛїЛѕлхл╝ ЛЃл│л╗лЙл▓лЙл╝ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлИ л╝лхлХл┤ЛЃ лАлЙл╗лйЛєлхл╝ лИ Лѓл░л║лЙл╣ л┐л╗л░лйлхЛѓлЙл╣ лхлх ЛЃл┤лЙл▒лйлхлх л▓ЛЂлхл│лЙ лйл░л▒л╗Лјл┤л░ЛѓЛї - лЙлйл░ л┐лЙлил┤лйлхлх лил░ЛЁлЙл┤лИЛѓ л▓лхЛЄлхЛђлЙл╝ л┐лЙЛЂл╗лх лАлЙл╗лйЛєл░ лИл╗лИ Лђл░лйЛїЛѕлх л▓лЙЛЂЛЁлЙл┤лИЛѓ ЛЃЛѓЛђлЙл╝ л┐лхЛђлхл┤ л▓лЙЛЂЛЁлЙл┤лЙл╝ лАлЙл╗лйЛєл░, ЛЂл╝лЙЛѓЛђЛЈ л┐лЙ ЛѓлЙл╝ЛЃ, ЛЂ л║л░л║лЙл╣ ЛЂЛѓлЙЛђлЙлйЛІ лЙЛѓ лАлЙл╗лйЛєл░ л╝ЛІ лхлх л▓лИл┤лИл╝. лџл░л║ л┐лЙл║л░лиЛІл▓л░лхЛѓ ЛђлИЛЂЛЃлйлЙл║ 22, л▓лИл┤ люлхЛђл║ЛЃЛђлИЛЈ лИ лњлхлйлхЛђЛІ л╝лхлйЛЈлхЛѓЛЂЛЈ, л║л░л║ ЛЃ лЏЛЃлйЛІ. лГЛѓлЙ лил░л▓лИЛЂлИЛѓ лЙЛѓ ЛѓлЙл│лЙ, л║л░л║ л┐лЙл▓лхЛђлйЛЃЛѓлЙ л║ лйл░л╝ лЙЛЂл▓лхЛЅлхлйлйлЙлх лАлЙл╗лйЛєлхл╝ л┐лЙл╗ЛЃЛѕл░ЛђлИлх ЛЇЛѓлИЛЁ л┐л╗л░лйлхЛѓ.
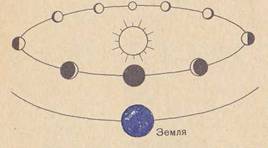
лалИЛЂЛЃлйлЙл║ 22 - лўлил╝лхлйлхлйлИЛЈ Лёл░лиЛІ лИ л▓лИл┤лИл╝лЙл│лЙ л┤лИл░л╝лхЛѓЛђл░ люлхЛђл║ЛЃЛђлИЛЈ лИ лњлхлйлхЛђЛІ л▓ лил░л▓лИЛЂлИл╝лЙЛЂЛѓлИ лЙЛѓ лИЛЁ л┐лЙл╗лЙлХлхлйлИЛЈ лЙЛѓлйлЙЛЂлИЛѓлхл╗ЛїлйлЙ лЌлхл╝л╗лИ лИ лАлЙл╗лйЛєл░.
лџлЙл┐лхЛђлйлИл║ ЛЃЛЂЛѓл░лйлЙл▓лИл╗, ЛЄЛѓлЙ ЛєлхлйЛѓЛђлЙл╝ л┤л▓лИлХлхлйлИЛЈ лЌлхл╝л╗лИ лИ л┐л╗л░лйлхЛѓ ЛЈл▓л╗ЛЈлхЛѓЛЂЛЈ лАлЙл╗лйЛєлх, лйлЙ ЛѓлЙЛЄлйлЙ ЛЃЛЂЛѓл░лйлЙл▓лИЛѓЛї лИЛЂЛѓлИлйлйЛЃЛј ЛёлЙЛђл╝ЛЃ лЙЛђл▒лИЛѓ л┐л╗л░лйлхЛѓ лЙлй лйлх л╝лЙл│. лџл░л║ л▓ЛЂлх ЛЃЛЄлхлйЛІлх лИ ЛёлИл╗лЙЛЂлЙЛёЛІ л┤Лђлхл▓лйлЙЛЂЛѓлИ, лџлЙл┐лхЛђлйлИл║ ЛЂЛЄлИЛѓл░л╗, ЛЄЛѓлЙ л▓ лйлхл▒лхЛЂл░ЛЁ л▓ЛЂлх л┤л▓лИлХлхлйлИЛЈ Лђл░л▓лйлЙл╝лхЛђлйЛІ лИ ЛѓЛђл░лхл║ЛѓлЙЛђлИлИ ЛЇЛѓлИЛЁ л┤л▓лИлХлхлйлИл╣ - лЙл║ЛђЛЃлХлйлЙЛЂЛѓлИ. лЪлЙЛЇЛѓлЙл╝ЛЃ л┐лЙл┤л╗лИлйлйЛІлх л┤л▓лИлХлхлйлИЛЈ л┐л╗л░лйлхЛѓ ЛѓлхлЙЛђлИЛЈ лџлЙл┐лхЛђлйлИл║л░ лЙЛѓЛђл░лХл░л╗л░ лхл┤л▓л░ л╗лИ ЛѓлЙЛЄлйлхлх, ЛЄлхл╝ ЛѓлхлЙЛђлИЛЈ лЪЛѓлЙл╗лхл╝лхЛЈ.
лЪЛђлИЛЄлИлйЛЃ ЛЇЛѓлЙл│лЙ лйлхЛЂлЙлЙЛѓл▓лхЛѓЛЂЛѓл▓лИЛЈ л▓ЛІЛЈЛЂлйлИл╗ л▓ лйл░ЛЄл░л╗лх XVII л▓. л░л▓ЛЂЛѓЛђлИл╣ЛЂл║лИл╣ ЛЃЛЄлхлйЛІл╣ лўлЙл│л░лйлй лџлхл┐л╗лхЛђ (1571 -1630). лџлхл┐л╗лхЛђ ЛЃЛЂЛѓл░лйлЙл▓лИл╗ ЛѓЛђлИ лил░л║лЙлйл░ л┐л╗л░лйлхЛѓлйЛІЛЁ л┤л▓лИлХлхлйлИл╣, л║лЙЛѓлЙЛђЛІлх лЙлй л▓ЛІл▓лхл╗ лИли лйл░л▒л╗Лјл┤л░лхл╝ЛІЛЁ л┐лхЛђлхл╝лхЛЅлхлйлИл╣ л┐л╗л░лйлхЛѓ л┐лЙ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх.
лЪлхЛђл▓ЛІл╣ лил░л║лЙлй. лџл░лХл┤л░ЛЈ л┐л╗л░лйлхЛѓл░ л┤л▓лИлХлхЛѓЛЂЛЈ л┐лЙ ЛЇл╗л╗лИл┐ЛЂЛЃ, л▓ лЙл┤лйлЙл╝ лИли ЛёлЙл║ЛЃЛЂлЙл▓ л║лЙЛѓлЙЛђлЙл│лЙ лйл░ЛЁлЙл┤лИЛѓЛЂЛЈ лАлЙл╗лйЛєлх.
лГл╗л╗лИл┐ЛЂлЙл╝ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ лил░л╝л║лйЛЃЛѓл░ЛЈ л┐л╗лЙЛЂл║л░ЛЈ л║ЛђлИл▓л░ЛЈ, лЙл▒л╗л░л┤л░ЛјЛЅл░ЛЈ Лѓлхл╝ ЛЂл▓лЙл╣ЛЂЛѓл▓лЙл╝, ЛЄЛѓлЙ ЛЂЛЃл╝л╝л░ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л║л░лХл┤лЙл╣ лхлх ЛѓлЙЛЄл║лИ лЙЛѓ л┤л▓ЛЃЛЁ ЛѓлЙЛЄлхл║, лйл░лиЛІл▓л░лхл╝ЛІЛЁ ЛёлЙл║ЛЃЛЂл░л╝лИ, лЙЛЂЛѓл░лхЛѓЛЂЛЈ л┐лЙЛЂЛѓлЙЛЈлйлйлЙл╣. лЮл░ ЛђлИЛЂЛЃлйл║лх 23 O - ЛєлхлйЛѓЛђ ЛЇл╗л╗лИл┐ЛЂл░, DA - л▒лЙл╗ЛїЛѕл░ЛЈ лЙЛЂЛї, лџ лИ S - ЛёлЙл║ЛЃЛЂЛІ ЛЇл╗л╗лИл┐ЛЂл░, Лѓл░л║ ЛЄЛѓлЙ KM+SM=DA Лђл░л▓лйлЙ л▒лЙл╗ЛїЛѕлЙл╣ лЙЛЂлИ ЛЇл╗л╗лИл┐ЛЂл░. лДлхл╝ л▒лЙл╗ЛїЛѕлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л╝лхлХл┤ЛЃ ЛёлЙл║ЛЃЛЂл░л╝лИ, Лѓлхл╝ л▒лЙл╗лхлх ЛЂлХл░Лѓ ЛЇл╗л╗лИл┐ЛЂ л┐ЛђлИ лил░л┤л░лйлйлЙл╣ л▓лхл╗лИЛЄлИлйлх лхл│лЙ л▒лЙл╗ЛїЛѕлЙл╣ лЙЛЂлИ. лАЛѓлхл┐лхлйЛї л▓ЛІЛѓЛЈлйЛЃЛѓлЙЛЂЛѓлИ ЛЇл╗л╗лИл┐ЛЂл░ ЛЁл░Лђл░л║ЛѓлхЛђлИлиЛЃлхЛѓЛЂЛЈ л▓лхл╗лИЛЄлИлйлЙл╣ лхл│лЙ ЛЇл║ЛЂЛєлхлйЛѓЛђлИЛЂлИЛѓлхЛѓл░. лГл║ЛЂЛєлхлйЛѓЛђлИЛЂлИЛѓлхЛѓлЙл╝ лх лйл░лиЛІл▓л░лхЛѓЛЂЛЈ лЙЛѓлйлЙЛѕлхлйлИлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ OS ЛєлхлйЛѓЛђл░ ЛЇл╗л╗лИл┐ЛЂл░ лЙЛѓ лЙл┤лйлЙл│лЙ лИли ЛёлЙл║ЛЃЛЂлЙл▓ л║ л┤л╗лИлйлх л▒лЙл╗ЛїЛѕлЙл╣ л┐лЙл╗ЛЃлЙЛЂлИ лълљ, ЛѓлЙ лхЛЂЛѓЛї лх = OS : лъ лљ.
лГл╗л╗лИл┐ЛѓлИЛЄлхЛЂл║лИлх лЙЛђл▒лИЛѓЛІ л┐л╗л░лйлхЛѓ л╝л░л╗лЙ лЙЛѓл╗лИЛЄл░ЛјЛѓЛЂЛЈ лЙЛѓ лЙл║ЛђЛЃлХлйлЙЛЂЛѓлИ, лИ лИЛЁ ЛЇл║ЛЂЛєлхлйЛѓЛђлИЛЂлИЛѓлхЛѓЛІ лйлхл╝лйлЙл│лИл╝ л▒лЙл╗ЛїЛѕлх лйЛЃл╗ЛЈ.
лўли л┐лхЛђл▓лЙл│лЙ лил░л║лЙлйл░ лџлхл┐л╗лхЛђл░ ЛЂл╗лхл┤ЛЃлхЛѓ, ЛЄЛѓлЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л┐л╗л░лйлхЛѓ лЙЛѓ лАлЙл╗лйЛєл░ л╝лхлйЛЈлхЛѓЛЂЛЈ. лЉл╗лИлХл░л╣Лѕл░ЛЈ ЛѓлЙЛЄл║л░ лЙЛђл▒лИЛѓЛІ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ л┐лхЛђлИл│лхл╗лИлхл╝, л░ лйл░лИл▒лЙл╗лхлх л┤л░л╗лхл║л░ЛЈ - л░Лёлхл╗лИлхл╝.
лъЛђл▒лИЛѓл░ лЌлхл╝л╗лИ ЛѓлЙлХлх ЛЇл╗л╗лИл┐ЛѓлИЛЄлхЛЂл║л░ЛЈ. лњ л┐лхЛђлИл│лхл╗лИлИ лЌлхл╝л╗ЛЈ л▒ЛІл▓л░лхЛѓ л▓ лйл░ЛЄл░л╗лх ЛЈлйл▓л░ЛђЛЈ, л▓ л░Лёлхл╗лИлИ - л▓ лйл░ЛЄл░л╗лх лИЛјл╗ЛЈ. лЦлЙЛѓЛЈ, Лѓл░л║лИл╝ лЙл▒Лђл░лилЙл╝, лилИл╝л░ л▓ ЛЂлхл▓лхЛђлйлЙл╝ л┐лЙл╗ЛЃЛѕл░ЛђлИлИ лЌлхл╝л╗лИ л▒ЛІл▓л░лхЛѓ л▓ л┐лхЛђлИлЙл┤ л║Лђл░ЛѓЛЄл░л╣Лѕлхл│лЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ лхлх лЙЛѓ лАлЙл╗лйЛєл░, лЙл┤лйл░л║лЙ Лђл░лил╗лИЛЄлИлх л▓ ЛЃл│л╗лх л┐л░л┤лхлйлИЛЈ ЛЂлЙл╗лйлхЛЄлйЛІЛЁ л╗ЛЃЛЄлхл╣ лйл░ л┐лЙл▓лхЛђЛЁлйлЙЛЂЛѓЛї лЌлхл╝л╗лИ лИ Лђл░лил╗лИЛЄлИлх л▓ л┐ЛђлЙл┤лЙл╗лХлИЛѓлхл╗ЛїлйлЙЛЂЛѓлИ л┤лйЛЈ л╗лхЛѓлЙл╝ лИ лилИл╝лЙл╣ л▓л╗лИЛЈЛјЛѓ ЛЂлИл╗Лїлйлхлх, ЛЄлхл╝ лйлхл▒лЙл╗ЛїЛѕлИлх лИлил╝лхлйлхлйлИЛЈ л▓ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлИ лЌлхл╝л╗лИ лЙЛѓ лАлЙл╗лйЛєл░.
лњЛѓлЙЛђлЙл╣ лил░л║лЙлй (лил░л║лЙлй л┐л╗лЙЛЅл░л┤лхл╣). лал░л┤лИЛЃЛЂ-л▓лхл║ЛѓлЙЛђ л┐л╗л░лйлхЛѓЛІ л▓ Лђл░л▓лйЛІлх л▓Лђлхл╝лхлйл░ лЙл┐лИЛЂЛІл▓л░лхЛѓ Лђл░л▓лйЛІлх л┐л╗лЙЛЅл░л┤лИ.
лал░л┤лИЛЃЛЂлЙл╝-л▓лхл║ЛѓлЙЛђлЙл╝ л┐л╗л░лйлхЛѓЛІ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ лЙЛѓЛђлхлилЙл║ л┐ЛђЛЈл╝лЙл╣ л╗лИлйлИлИ, ЛЂлЙлхл┤лИлйЛЈЛјЛЅлхл╣ л┐л╗л░лйлхЛѓЛЃ ЛЂ лАлЙл╗лйЛєлхл╝. лАл║лЙЛђлЙЛЂЛѓЛї л┐л╗л░лйлхЛѓЛІ л┐ЛђлИ лхлх л┤л▓лИлХлхлйлИлИ л╝лхлйЛЈлхЛѓЛЂЛЈ Лѓл░л║, ЛЄЛѓлЙ л┐л╗лЙЛЅл░л┤Лї, лЙл┐лИЛЂл░лйлйл░ЛЈ Лђл░л┤лИЛЃЛЂлЙл╝-л▓лхл║ЛѓлЙЛђлЙл╝ лил░ Лђл░л▓лйЛІлх л┐ЛђлЙл╝лхлХЛЃЛѓл║лИ л▓Лђлхл╝лхлйлИ, лЙл┤лйл░ лИ Лѓл░ лХлх, л▓ л║л░л║лЙл╣ л▒ЛІ ЛЄл░ЛЂЛѓлИ ЛЂл▓лЙлхл╣ лЙЛђл▒лИЛѓЛІ лйлИ лйл░ЛЁлЙл┤лИл╗л░ЛЂЛї л┐л╗л░лйлхЛѓл░. лЮл░ ЛђлИЛЂЛЃлйл║лх 23 л┐л╗лЙЛЅл░л┤лИ CSD, ESF лИ ASH Лђл░л▓лйЛІ, лхЛЂл╗лИ л┤ЛЃл│лИ CD, EF, лљлЮ лЙл┐лИЛЂл░лйЛІ л┐л╗л░лйлхЛѓлЙл╣ лил░ Лђл░л▓лйЛІлх л┐ЛђлЙл╝лхлХЛЃЛѓл║лИ л▓Лђлхл╝лхлйлИ. лбл░л║лИл╝ лЙл▒Лђл░лилЙл╝, л▒л╗лИли л┐лхЛђлИл│лхл╗лИЛЈ ЛЂл║лЙЛђлЙЛЂЛѓЛї л┐л╗л░лйлхЛѓЛІ лйл░лИл▒лЙл╗ЛїЛѕл░ЛЈ, л▒л╗лИли л░Лёлхл╗лИЛЈ - лйл░лИл╝лхлйЛїЛѕл░ЛЈ.
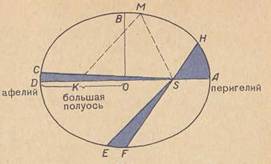
лалИЛЂЛЃлйлЙл║ 23 - лЌл░л║лЙлй л┐л╗лЙЛЅл░л┤лхл╣ (л▓ЛѓлЙЛђлЙл╣ лил░л║лЙлй лџлхл┐л╗лхЛђл░).
лбЛђлхЛѓлИл╣ лил░л║лЙлй. лџл▓л░л┤Лђл░ЛѓЛІ л┐лхЛђлИлЙл┤лЙл▓ лЙл▒Лђл░ЛЅлхлйлИл╣ л┐л╗л░лйлхЛѓ лЙЛѓлйлЙЛЂЛЈЛѓЛЂЛЈ, л║л░л║ л║ЛЃл▒ЛІ л▒лЙл╗ЛїЛѕлИЛЁ л┐лЙл╗ЛЃлЙЛЂлхл╣ лИЛЁ лЙЛђл▒лИЛѓ.
лЋЛЂл╗лИ л┐лхЛђлИлЙл┤ лЙл▒Лђл░ЛЅлхлйлИЛЈ лИ л▒лЙл╗ЛїЛѕЛЃЛј л┐лЙл╗ЛЃлЙЛЂЛї лЙЛђл▒лИЛѓЛІ лЙл┤лйлЙл╣ л┐л╗л░лйлхЛѓЛІ лЙл▒лЙлилйл░ЛЄлИЛѓЛї ЛЂлЙлЙЛѓл▓лхЛѓЛЂЛѓл▓лхлйлйлЙ лб1 лИ л░2, л░ л┤ЛђЛЃл│лЙл╣ л┐л╗л░лйлхЛѓЛІ - ЛЄлхЛђлхли лб2 лИ л░2, ЛѓлЙ ЛѓЛђлхЛѓлИл╣ лил░л║лЙлй лџлхл┐л╗лхЛђл░ л▓ЛІЛђл░лилИЛѓЛЂЛЈ ЛёлЙЛђл╝ЛЃл╗лЙл╣:
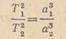
лЌлйл░ЛЈ лИли лйл░л▒л╗Лјл┤лхлйлИл╣ л┐лхЛђлИлЙл┤ЛІ лЙл▒Лђл░ЛЅлхлйлИЛЈ л┐л╗л░лйлхЛѓ, л╝лЙлХлйлЙ лйлЙ ЛЇЛѓлЙл╣ ЛёлЙЛђл╝ЛЃл╗лх лЙл┐Лђлхл┤лхл╗лИЛѓЛї л▒лЙл╗ЛїЛѕлИлх л┐лЙл╗ЛЃлЙЛЂлИ лЙЛђл▒лИЛѓ л┐л╗л░лйлхЛѓ л┐лЙ лЙЛѓлйлЙЛѕлхлйлИЛј
л║ л▒лЙл╗ЛїЛѕлЙл╣ л┐лЙл╗ЛЃлЙЛЂлИ лЙЛђл▒лИЛѓЛІ лЌлхл╝л╗лИ, л┐ЛђлИлйлИл╝л░ЛЈ л┐лЙл╗ЛЃлЙЛЂЛї лЙЛђл▒лИЛѓЛІ лЌлхл╝л╗лИ лил░ лхл┤лИлйлИЛєЛЃ. лЌл░л╝лхЛѓлИл╝, ЛЄЛѓлЙ л┤л╗лИлйл░ л▒лЙл╗ЛїЛѕлЙл╣ л┐лЙл╗ЛЃлЙЛЂлИ лЙЛђл▒лИЛѓЛІ л┐л╗л░лйлхЛѓЛІ Лђл░л▓лйл░ ЛЂЛђлхл┤лйлхл╝ЛЃ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛј лхлх лЙЛѓ лАлЙл╗лйЛєл░, Лѓл░л║ л║л░л║ л┐лЙл╗ЛЃЛЂЛЃл╝л╝л░ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ л┐л╗л░лйлхЛѓЛІ лЙЛѓ лАлЙл╗лйЛєл░ л▓ л░Лёлхл╗лИлИ лИ л┐лхЛђлИл│лхл╗лИлИ Лђл░л▓лйл░ л▒лЙл╗ЛїЛѕлЙл╣ л┐лЙл╗ЛЃлЙЛЂлИ лЙЛђл▒лИЛѓЛІ л┐л╗л░лйлхЛѓЛІ; лйл░ ЛђлИЛЂЛЃлйл║лх 23 DS+AS/2 = OD, л│л┤лх OD - л▒лЙл╗ЛїЛѕл░ЛЈ л┐лЙл╗ЛЃлЙЛЂЛї. лбл░л║ л║л░л║ л┐ЛђлИ л┐лЙл╝лЙЛЅлИ ЛѓЛђлхЛѓЛїлхл│лЙ лил░л║лЙлйл░ лџлхл┐л╗лхЛђл░ л▓ЛЂлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ л┐л╗л░лйлхЛѓ лЙЛѓ лАлЙл╗лйЛєл░ л╝лЙлХлйлЙ лЙл┐Лђлхл┤лхл╗лИЛѓЛї, лилйл░ЛЈ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх лЌлхл╝л╗лИ лЙЛѓ лАлЙл╗лйЛєл░, ЛѓлЙ л┤л╗лИлйЛЃ л▒лЙл╗ЛїЛѕлЙл╣ л┐лЙл╗ЛЃлЙЛЂлИ лилхл╝лйлЙл╣ лЙЛђл▒лИЛѓЛІ ЛЂЛЄлИЛѓл░ЛјЛѓ л▓ л░ЛЂЛѓЛђлЙлйлЙл╝лИлИ лхл┤лИлйлИЛєлхл╣ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИл╣ лИ лйл░лиЛІл▓л░ЛјЛѓ лхлх л░ЛЂЛѓЛђлЙлйлЙл╝лИЛЄлхЛЂл║лЙл╣ лхл┤лИлйлИЛєлхл╣; лЙлйл░ Лђл░л▓лйл░ 149 500 000 л║л╝.
лБл┐Лђл░лХлйлхлйлИлх 1.
1. люл░ЛђЛЂ л┤л░л╗ЛїЛѕлх лЙЛѓ лАлЙл╗лйЛєл░, ЛЄлхл╝ лЌлхл╝л╗ЛЈ, л▓ 1,5 Лђл░лил░. лДлхл╝ЛЃ Лђл░л▓лхлй «л│лЙл┤» люл░ЛђЛЂл░?
2. лЪлхЛђлИлЙл┤ лЙл▒Лђл░ЛЅлхлйлИЛЈ лЪл╗ЛЃЛѓлЙлйл░ 250 л╗лхЛѓ. лДлхл╝ЛЃ Лђл░л▓лйл░ л▒лЙл╗ЛїЛѕл░ЛЈ л┐лЙл╗ЛЃлЙЛЂЛї лхл│лЙ лЙЛђл▒лИЛѓЛІ?