лЮлхл▒лхЛЂлйл░ЛЈ ЛЂЛёлхЛђл░ лИ лхлх лилйл░ЛЄлхлйлИЛЈ л┤л╗ЛЈ л┐Лђл░л║ЛѓлИл║лИ
1. лЮлхл▒лхЛЂлйл░ЛЈ ЛЂЛёлхЛђл░. лњЛЂлх лйлхл▒лхЛЂлйЛІлх ЛЂл▓лхЛѓлИл╗л░ л║л░лХЛЃЛѓЛЂЛЈ лЙл┤лИлйл░л║лЙл▓лЙ л┤л░л╗лхл║лИл╝лИ лЙЛѓ лйл░ЛЂ, ЛЁлЙЛѓЛЈ лИЛЂЛѓлИлйлйЛІлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ л┤лЙ лил▓лхлил┤ лЙЛЄлхлйЛї Лђл░лил╗лИЛЄлйЛІ. лћл╗ЛЈ л│л╗л░лил░ ЛЇЛѓлЙ Лђл░лил╗лИЛЄлИлх л▓ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈЛЁ ЛЂлЙл▓лхЛђЛѕлхлйлйлЙ лйлхлил░л╝лхЛѓлйлЙ. лЪлЙЛЇЛѓлЙл╝ЛЃ ЛЃл┤лЙл▒лйлЙ Лђл░ЛЂЛЂл╝л░ЛѓЛђлИл▓л░ЛѓЛї лил▓лхлил┤ЛІ ЛЃЛЂл╗лЙл▓лйлЙ л║л░л║ л▒ЛІ лйл░ЛЁлЙл┤ЛЈЛЅлИл╝лИЛЂЛЈ лйл░ л▓лйЛЃЛѓЛђлхлйлйлхл╣ л┐лЙл▓лхЛђЛЁлйлЙЛЂЛѓлИ Лѕл░Лђл░ л┐ЛђлЙлИлил▓лЙл╗ЛїлйлЙл│лЙ Лђл░л┤лИЛЃЛЂл░, л▓ ЛєлхлйЛѓЛђлх л║лЙЛѓлЙЛђлЙл│лЙ лйл░ЛЁлЙл┤лИЛѓЛЂЛЈ л│л╗л░ли лйл░л▒л╗Лјл┤л░Лѓлхл╗ЛЈ. лЮлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлЙл╣ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ л▓лЙлЙл▒Лђл░лХл░лхл╝л░ЛЈ Лѕл░ЛђлЙл▓л░ЛЈ л┐лЙл▓лхЛђЛЁлйлЙЛЂЛѓЛї л┐ЛђлЙлИлил▓лЙл╗ЛїлйлЙл│лЙ Лђл░л┤лИЛЃЛЂл░, лйл░ л║лЙЛѓлЙЛђЛЃЛј л╝ЛІ л┐ЛђлЙлхл║ЛѓлИЛђЛЃлхл╝ л┐лЙл╗лЙлХлхлйлИлх лйлхл▒лхЛЂлйЛІЛЁ ЛЂл▓лхЛѓлИл╗.
лЪлЙлйЛЈЛѓлИлхл╝ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђЛІ л┐лЙл╗ЛїлиЛЃЛјЛѓЛЂЛЈ л┤л╗ЛЈ ЛЃл│л╗лЙл▓ЛІЛЁ лИлил╝лхЛђлхлйлИл╣ лйл░ лйлхл▒лх, л┤л╗ЛЈ ЛЃл┤лЙл▒ЛЂЛѓл▓л░ Лђл░ЛЂЛЂЛЃлХл┤лхлйлИл╣ лЙ л┐ЛђлЙЛЂЛѓлхл╣ЛѕлИЛЁ л▓лИл┤лИл╝ЛІЛЁ лйлхл▒лхЛЂлйЛІЛЁ ЛЈл▓л╗лхлйлИЛЈЛЁ, л░ Лѓл░л║лХлх л┤л╗ЛЈ Лђл░лил╗лИЛЄлйЛІЛЁ Лђл░ЛЂЛЄлхЛѓлЙл▓, лйл░л┐ЛђлИл╝лхЛђ л┤л╗ЛЈ л▓ЛІЛЄлИЛЂл╗лхлйлИЛЈ л▓Лђлхл╝лхлйлИ л▓лЙЛЂЛЁлЙл┤л░ лИ лил░ЛЁлЙл┤л░ ЛЂл▓лхЛѓлИл╗. лбл░л║лИл╝ лЙл▒Лђл░лилЙл╝, л┐лЙлйЛЈЛѓлИлх лЙ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх л┐ЛђлИлйлЙЛЂлИЛѓ л┐Лђл░л║ЛѓлИЛЄлхЛЂл║ЛЃЛј л┐лЙл╗ЛїлиЛЃ.
лал░ЛЂЛЂЛЃлХл┤л░ЛЈ лЙ л▓лЙЛЂЛЁлЙл┤лх, лил░ЛЁлЙл┤лх лИ л┤ЛђЛЃл│лИЛЁ л▓лИл┤лИл╝ЛІЛЁ лйлхл▒лхЛЂлйЛІЛЁ ЛЈл▓л╗лхлйлИЛЈЛЁ, л╝ЛІ ЛЂЛЄлИЛѓл░лхл╝ЛЂЛЈ л╗лИЛѕЛї ЛЂ лйл░л┐Лђл░л▓л╗лхлйлИлхл╝, л┐лЙ л║лЙЛѓлЙЛђлЙл╝ЛЃ л▓лИл┤лйЛІ ЛЂл▓лхЛѓлИл╗л░ (лйл░л┐ЛђлИл╝лхЛђ, л▒л╗лИли л│лЙЛђлИлилЙлйЛѓл░, лйл░л┤ л│лЙл╗лЙл▓лЙл╣ лИ Лѓ. л┤.), л┐лЙЛЇЛѓлЙл╝ЛЃ л▒лхлиЛђл░лил╗лИЛЄлйлЙ, л║л░л║лЙл╣ Лђл░л┤лИЛЃЛЂ л▓ЛІл▒Лђл░ЛѓЛї л┤л╗ЛЈ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђЛІ. лалИЛЂЛЃлйлЙл║ 11 л┐лЙл║л░лиЛІл▓л░лхЛѓ, ЛЄЛѓлЙ л╗Лјл▒л░ЛЈ лил▓лхлил┤л░, л▓лИл┤лИл╝л░ЛЈ лйл░л▒л╗Лјл┤л░Лѓлхл╗лхл╝ л┐лЙ л║л░л║лЙл╝ЛЃ-л╗лИл▒лЙ лйл░л┐Лђл░л▓л╗лхлйлИЛј, л▒ЛЃл┤лхЛѓ л▓лИл┤лйл░ л┐лЙ ЛЇЛѓлЙл╝ЛЃ лХлх лйл░л┐Лђл░л▓л╗лхлйлИЛј лйл░ ЛЂЛёлхЛђлх Лђл░л┤лИЛЃЛЂл░ R1 лИл╗лИ лйл░ ЛЂЛёлхЛђлх Лђл░л┤лИЛЃЛЂл░ R2. лЪлЙЛЇЛѓлЙл╝ЛЃ лИ л│лЙл▓лЙЛђЛЈЛѓ, ЛЄЛѓлЙ лйлхл▒лхЛЂлйл░ЛЈ ЛЂЛёлхЛђл░ лИл╝лхлхЛѓ л┐ЛђлЙлИлил▓лЙл╗ЛїлйЛІл╣ Лђл░л┤лИЛЃЛЂ.
2. лБл│л╗лЙл▓ЛІлх лИлил╝лхЛђлхлйлИЛЈ. лАЛЄлИЛѓл░ЛЈ ЛЃЛЂл╗лЙл▓лйлЙ л▓ЛЂлх ЛЂл▓лхЛѓлИл╗л░ Лђл░ЛЂл┐лЙл╗лЙлХлхлйлйЛІл╝лИ лйл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх (л▓лхЛђлйлхлх, л┐ЛђлЙлхл║ЛѓлИЛђЛЃЛЈ лИЛЁ лйл░ лйлхлх), л╝ЛІ л╝лЙлХлхл╝ лИлил╝лхЛђЛЈЛѓЛї ЛѓлЙл╗Лїл║лЙ ЛЃл│л╗ЛІ л╝лхлХл┤ЛЃ лйл░л┐Лђл░л▓л╗лхлйлИЛЈл╝лИ, л┐лЙ л║лЙЛѓлЙЛђЛІл╝ ЛЇЛѓлИ ЛЂл▓лхЛѓлИл╗л░ л▓лИл┤лйЛІ. лГЛѓлИл╝ ЛЃл│л╗л░л╝ лйл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх ЛЂлЙлЙЛѓл▓лхЛѓЛЂЛѓл▓ЛЃЛјЛѓ л┤ЛЃл│лИ л▒лЙл╗ЛїЛѕлИЛЁ л║ЛђЛЃл│лЙл▓ (л▒лЙл╗ЛїЛѕлИл╝ л║ЛђЛЃл│лЙл╝ ЛЂЛёлхЛђЛІ лйл░лиЛІл▓л░лхЛѓЛЂЛЈ л▓ЛЂЛЈл║лИл╣ л║ЛђЛЃл│, ЛєлхлйЛѓЛђ л║лЙЛѓлЙЛђлЙл│лЙ ЛЂлЙл▓л┐л░л┤л░лхЛѓ ЛЂ ЛєлхлйЛѓЛђлЙл╝ ЛЂЛёлхЛђЛІ). лЮл░л┐ЛђлИл╝лхЛђ, л╝ЛІ л│лЙл▓лЙЛђлИл╝, ЛЄЛѓлЙ лил▓лхлил┤ЛІ лљ лИ лњ (лалИЛЂЛЃлйлЙл║ 11) лЙЛѓЛЂЛѓлЙЛЈЛѓ лйл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх лЙл┤лйл░ лЙЛѓ л┤ЛђЛЃл│лЙл╣ лйл░ 23°, лхЛЂл╗лИ ЛЃл│лЙл╗ л╝лхлХл┤ЛЃ лйл░л┐Лђл░л▓л╗лхлйлИЛЈл╝лИ лАлљ лИ лАлњ лйл░ ЛЇЛѓлИ лил▓лхлил┤ЛІ Лђл░л▓лхлй 23°. лЮл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх ЛЇЛѓлЙл╝ЛЃ ЛЃл│л╗ЛЃ ЛЂлЙлЙЛѓл▓лхЛѓЛЂЛѓл▓ЛЃлхЛѓ л┤ЛЃл│л░ лљ1лњ1 Лђл░л▓лйл░ЛЈ 23°. лЌл▓лхлил┤л░ лљ л╝лЙлХлхЛѓ л▒ЛІЛѓЛї лЙЛѓ лйл░ЛЂ л│лЙЛђл░лил┤лЙ л┤л░л╗ЛїЛѕлх, ЛЄлхл╝ лил▓лхлил┤л░ D, лйлЙ лхЛЂл╗лИ лЙл▒лх лЙлйлИ л▓лИл┤лйЛІ л┐лЙЛЄЛѓлИ л┐лЙ лЙл┤лйлЙл╝ЛЃ лИ ЛѓлЙл╝ЛЃ лХлх лйл░л┐Лђл░л▓л╗лхлйлИЛј, л╝ЛІ л│лЙл▓лЙЛђлИл╝, ЛЄЛѓлЙ лйл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх лил▓лхлил┤л░ D лилйл░ЛЄлИЛѓлхл╗ЛїлйлЙ л▒л╗лИлХлх л║ лил▓лхлил┤лх лљ, ЛЄлхл╝ л║ лил▓лхлил┤лх лњ, ЛЁлЙЛѓЛЈ л▓ л┐ЛђлЙЛЂЛѓЛђл░лйЛЂЛѓл▓лх л╗лИлйлхл╣лйлЙлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх (л┤лЙл┐ЛЃЛЂЛѓлИл╝, л▓ л║лИл╗лЙл╝лхЛѓЛђл░ЛЁ) лЙЛѓ D л┤лЙ лљ л╝лЙлХлхЛѓ л▒ЛІЛѓЛї л│лЙЛђл░лил┤лЙ л▒лЙл╗ЛїЛѕлх, ЛЄлхл╝ лЙЛѓ D л┤лЙ лњ.
лЪлЙл┤лЙл▒лйлЙ ЛЇЛѓлЙл╝ЛЃ, лАлЙл╗лйЛєлх лИ лЏЛЃлйл░ лИл╝лхЛјЛѓ л┐лЙЛЄЛѓлИ лЙл┤лИлйл░л║лЙл▓ЛІл╣ л▓лИл┤лИл╝ЛІл╣ ЛЃл│л╗лЙл▓лЙл╣ л┤лИл░л╝лхЛѓЛђ (лЙл║лЙл╗лЙ л┐лЙл╗л│Лђл░л┤ЛЃЛЂл░), ЛЁлЙЛѓЛЈ л╗лИлйлхл╣лйЛІл╣ л┤лИл░л╝лхЛѓЛђ лЏЛЃлйЛІ л┐лЙЛЄЛѓлИ л▓ 400 Лђл░ли л╝лхлйЛїЛѕлх ЛЂлЙл╗лйлхЛЄлйлЙл│лЙ. лЌл░ЛѓлЙ лЙлйл░ л▓лЙ ЛЂЛѓлЙл╗Лїл║лЙ лХлх Лђл░ли л▒л╗лИлХлх л║ лйл░л╝, ЛЄлхл╝ лАлЙл╗лйЛєлх, лИ л┐лЙЛЇЛѓлЙл╝ЛЃ л║л░лХлхЛѓЛЂЛЈ лЙл┤лИлйл░л║лЙл▓лЙл│лЙ ЛЂ лйлИл╝ ЛЃл│л╗лЙл▓лЙл│лЙ Лђл░лил╝лхЛђл░. лЉлхЛЂЛЂл╝ЛІЛЂл╗лхлйлйлЙ ЛЂЛђл░л▓лйлИл▓л░ЛѓЛї л▓лИл┤лИл╝ЛІл╣ ЛЃл│л╗лЙл▓лЙл╣ л┤лИл░л╝лхЛѓЛђ лЏЛЃлйЛІ ЛЂ л║лЙл┐лхл╣л║лЙл╣ лИл╗лИ ЛЂ Лѓл░Лђлхл╗л║лЙл╣, лхЛЂл╗лИ лйлх лЙЛѓлйлхЛЂЛѓлИ л┐лЙЛЂл╗лхл┤лйлИлх л║ л║л░л║лЙл╝ЛЃ-л╗лИл▒лЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛј. лблЙЛЄлйлЙ Лѓл░л║ лХлх л▒лхЛЂЛЂл╝ЛІЛЂл╗лхлйлйЛІ л▓ЛІЛђл░лХлхлйлИЛЈ л▓ЛђлЙл┤лх: «лЏЛЃлйл░ л┐лЙл┤лйЛЈл╗л░ЛЂЛї лйл░ л┐лЙл╗л╝лхЛѓЛђл░ лйл░л┤ л│лЙЛђлИлилЙлйЛѓлЙл╝» лИл╗лИ «лъЛѓ лЙл┤лйлЙл╣ лил▓лхлил┤ЛІ л┤лЙ л┤ЛђЛЃл│лЙл╣ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх лйл░ лйлхл▒лх 2 л╝».
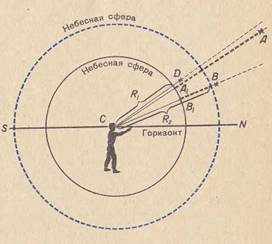
лалИЛЂЛЃлйлЙл║ 11 - лЪЛђлЙлхл║ЛѓлИЛђлЙл▓л░лйлИлх ЛЂл▓лхЛѓлИл╗ лйл░ лйлхл▒лхЛЂлйЛЃЛј ЛЂЛёлхЛђЛЃ.
лўЛѓл░л║, лйл░ лйлхл▒лхЛЂлйлЙл╣ ЛЂЛёлхЛђлх л╝лЙлХлйлЙ л┐ЛђлЙлИлил▓лЙл┤лИЛѓЛї ЛѓлЙл╗Лїл║лЙ ЛЃл│л╗лЙл▓ЛІлх лИлил╝лхЛђлхлйлИЛЈ.
лЋЛЂл╗лИ, л▓ЛІЛѓЛЈлйЛЃл▓ ЛђЛЃл║ЛЃ, Лђл░ЛЂЛЂЛѓл░л▓лИЛѓЛї л▒лЙл╗ЛїЛѕлЙл╣ лИ ЛЃл║л░лил░Лѓлхл╗ЛїлйЛІл╣ л┐л░л╗ЛїЛєЛІ, ЛѓлЙ Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л╝лхлХл┤ЛЃ л║лЙлйЛєл░л╝лИ л┐л░л╗ЛїЛєлхл▓ ЛЄлхл╗лЙл▓лхл║ ЛЃл▓лИл┤лИЛѓ л┐лЙл┤ ЛЃл│л╗лЙл╝ л┐ЛђлИл╝лхЛђлйлЙ 16°. лбл░л║лЙл╣ «ЛЃл│л╗лЙл▓лЙл╣ ЛЄлхЛѓл▓лхЛђЛѓЛїЛј» л╝лЙлХлйлЙ, л┐Лђл░л▓л┤л░ лЙЛЄлхлйЛї л│ЛђЛЃл▒лЙ, лИлил╝лхЛђЛЈЛѓЛї ЛЃл│л╗лЙл▓ЛІлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИЛЈ. лЪлЙл╗лхлилйлЙ лилйл░ЛѓЛї, ЛЄЛѓлЙ ЛЃл│л╗лЙл▓лЙлх Лђл░ЛЂЛЂЛѓлЙЛЈлйлИлх л╝лхлХл┤ЛЃ лил▓лхлил┤л░л╝лИ лљл╗ЛїЛёл░ лИ лЉлхЛѓл░ лЉлЙл╗ЛїЛѕлЙл╣ люлхл┤л▓лхл┤лИЛєЛІ Лђл░л▓лйлЙ 5°.